Закон Цикличности Времени. МАТРИЦА. Магический Кристалл

Джи.Н писал(а): Вот честно, картинку вы сохранили?

Матрицу Вашу? А то!

Джи.Н писал(а): Почему хозяин поступил так

Упрямые они. Самодельщики. Меня вот, тоже не слушаются.

Джи.Н писал(а): Собака Бык Дракон Коза объединены в социальную структуру. Совпадение или закономерность.

Не знаю, не думал. Хотя, зная, что тот же день попадает на то же число через 16 лет, мог и предположить.

Сообщение **Джи.Н** » 28 окт 2007, 22:24

Шриман писал(а): Упрямые они. Самодельщики. Меня вот, тоже не слушаются.

Фигушки!
Упоминаемый случай - Коза-Близнецы дала команду Тигру-Овен

Рисунок/images/smil-ti/icon_razz.gif

Джи.Н писал(а):Коза-Близнецы дала команду Тигру-Овен

Ну, так это, батенька, совсем классика. ТИГРА обидеть всяк норовит. Вспомните, как Ельцин третировал Коржакова, Лебедя, Черномырдина. Кириенку подставил ни за что, ни про што. Юань Ши Кай одолел Сунь Ят Сена, и т.п. Деликатный, воспитанный ТИГР вообще беззащитен против хама-КОЗЛА. ТИГРОВ любить и беречь надо.

Шриман писал(а):Так называемая «структура спасителя». На круговой схеме представляет 2 замкнутых кольца, пересекающихся в одном месте. Решили не публиковать.

Вот, нашёл в архивах. Господи, чего там только нет.

azasello писал(а):и что это за структура? не понимаю закономерности и действия.

Ну это, собственно для Джи.Н'а, из неопубликованного.
Спаситель это хозяин хозяина, нейтрализатор типа. Я, например, КОЗА. Хозяин мой ТГ, слуга ЗМ. Соответственно мой спаситель БК, я спаситель для ОБ. А ТГ спаситель для ЗМ.
При интерличностном взаимодействии структура практически не проявляется и была почти забыта, однако неожиданно мощно проявилась при анализе взаимодействия с текущем временем. В отличии от Векторного кольца, одного кольца не получается, а образуются два, делящие 12-летку пополам. При этом БК залезает на чужую половину, ему в отместку – ЗМ. Сейчас эту тему Джи.Н окучивает.

Сообщение **antol** » 31 окт 2007, 15:22

"На круговой схеме представляет 2 замкнутых кольца, пересекающихся в одном месте."
Какое это "одно место" пересечения, лично мне, из представленной картинки не понятно.

Рисунок/images/smil-ti/icon_question.gif

antol писал(а):Какое это "одно место"

писал по памяти, не видя схемы

Сообщение **antol** » 31 окт 2007, 16:05

некоторое абстрактное дополнение

Мы имеем операцию определения хозяина для знака СГ. И эта операция может быть вложенной.
Например Кб = хозяин Др = хозяин(хозяин Кт);
Или в более компактной форме записи, при двукратной вложенности выполнения этой операции получаем два "кольца" объединяющие по шесть знаков СГ:
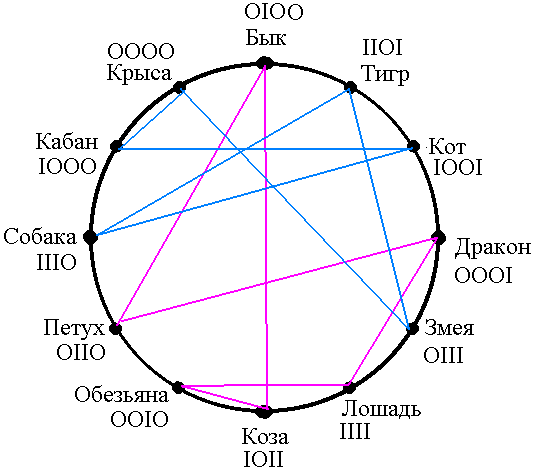
Кб = ххКт; Кт = ххСб; Сб = ххТг; Тг = ххЗм; Зм = ххКр; Кр = ххКб;
Бк = ххКз; Кз = ххОб; Об = ххЛш; Лш = ххДр; Др = ххПт; Пт = ххБк;
Эти "кольца" изображены на схеме, линиями голубого и розового цвета.

А что будем иметь, если продолжим выполнение операции, определения знака хозяина для хозяина?

Рисунок/images/smil-ti/icon_question.gif

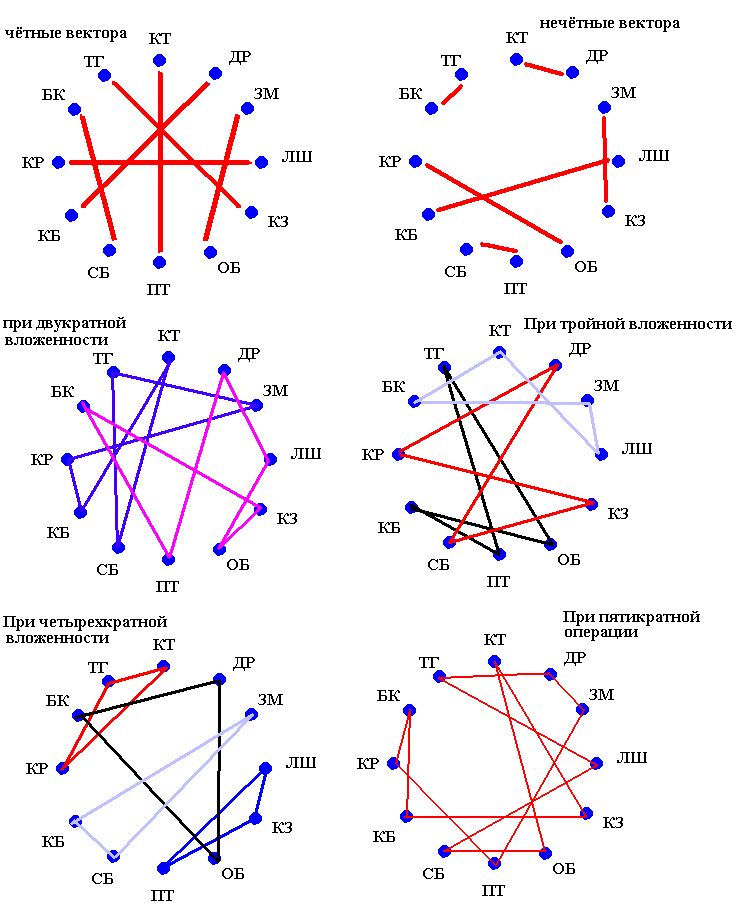
При тройной вложенности операции получим три кольца объединяющие по четыре знака СГ:
Кб = хххПт; Пт = хххТг; Тг = хххОб; Об = хххКб;
Кр = хххДр; Др = хххСб; Сб = хххКз; Кз = хххКр;
Бк = хххЗм; Зм = хххЛш; Лш = хххКт; Кт = хххБк;

При четырехкратной вложенности операции, знаки СГ объединяются в кольца по три:
Кб = ххххСб; Сб = ххххЗм; Зм = ххххКб;
Кр = ххххКт; Кт = ххххТг; Тг = ххххКр;
Бк = ххххОб; Об = ххххДр; Др = ххххБк;
Лш = ххххПт; Пт = ххххКз; Кз = ххххЛш;

При пятикратной операции получается одно кольцо, объединяющее все знаки.
Должно быть, потому, что 12 не делится на пять на цело.
- Кб - Бк - Кр - Пт - Зм - Др - Тг - Лш - Сб - Об - Кт - Кз -

При шестикратной вложенности операции знаки СГ объединяются в пары:
Кб = ххххххТг; Тг = ххххххКб;
Кр = ххххххСб; Сб = ххххххКр;
Бк = ххххххЛш; Лш = ххххххБк;
Кт = ххххххЗм; Зм = ххххххКт;
Др = ххххххКз; Кз = ххххххДр;
Об = ххххххПт; Пт = ххххххОб;

При 12-кратной вложенности, должно быть, в результате получим исходный знак.

"Решили не публиковать", тоже, блин.

Рисунок/images/smil-ti/icon_cry.gif

;-)

Сообщение **Джи.Н** » 31 окт 2007, 18:41

Сложно для восприятия и понимания. Честно..
А тему эту я уже окучил, ежели что...посмотрел мимоходом, отметил. что Шриман не прав и ушёл дальше.

antol писал(а):некоторое абстрактное дополнение

"Решили не публиковать", тоже, блин.

Н-да. Думать заставляет. Похоже, действительно что-то важное пропущено. Ежели всё это отложить на кольце с природной последовательностью, интересные вещи выплывают.

«При тройной вложенности операции получим три кольца»

3 подобные фигурки, в форме песочных часов. Причём каждая с каждой пересекается.

«При четырехкратной вложенности операции, знаки СГ объединяются в кольца по три»

при этом треугольнички КР – ТГ – КТ и ЛШ – КЗ – ПТ симметричны

«При пятикратной операции получается одно кольцо, объединяющее все знаки».

при этом подряд идут волевые знаки ЛШ – ТГ – СБ и реалисты КТ – КЗ – КБ.

Похоже, проклёвывается хоть какая-то симметрия в ВК. Пока, сходу, больше ничего не увидел. Буду думать дальше, похоже теперь моя очередь.